Race Against The Machine 讀後感

Race Against The Machine嚴格說來這並不是一本書, 而是幾個短章節組成的專文,類似一般雜誌中的專題探討之類。 我是看到Tim O’Reilly大叔在Google+上看到他簡短的推薦, 加上本身就有類似的想法決定看看是否有先進將我零碎的想法已經研究得透徹。
這篇專文主要是從一些經濟上的觀察開始講起, 包括了自金融海嘯以來,以往有效的貨幣手段似乎不再效果顯著, 儘管美國利率已經降到低到不行,資金放寬但消費就是起不來,失業率也居高不下。 同時間,美國各個教育水平的收入也在不停分化, 過去美國十年的增長,大部分增長的財富都集中在社會前百分之二十的人手上。 而且符合power law,越往前頭的百分比累積財富的速度越多。 作者認為撇除掉全球化,法規等因素讓原本在美國的低階工作流往海外等因素, 大家太輕忽了科技的影響力。 在這段時間,科技爆發性地成長,摩爾定律讓計算資源源源不絕地噴發出來。 導致許多工作都自動化,同樣的工作不再需要人。 他在第三章開頭就引用了凱因思的話:
We are being afflicted with a new disease of which some readers may not yet have heard the name, but of which they will hear a great deal in the years to come - namely, technological unemployment. This means unemployment due to our discovery of means of economising the use of labour outrunning the pace at which we can find new use for labour. - John Maynard Keynes, 1930
套到如今似乎也是如此適用。
機器不斷地在侵蝕原本我們認為是人專屬的領域,重點是這個勢頭來得如此之猛,讓我們的教育,政治組織架構來不及反應。 書中舉了幾個例子,包括Google的自動駕駛,IBM參加Joepardy超級電腦。 我們原本認為複雜的Pattern Recognition像是駕駛是非常難的,但現在的運算資源跟資料如此豐富讓我們可以達成這艱難的任務。 除了這些,我自己也看過好幾個例子。 像是我在Discovery上看過超級工廠系列。 有一集提到可口可樂操作整個裝瓶工場的人員不過是幾個人, 他們操作複雜的儀表控制整個工廠,包括精密的標籤機, 可以用雷射精準貼瓶到幾mm,如果超過標準就要放棄。 或是像海尼根在荷蘭的工廠,裡面從裝好瓶的機器搬運到貨車上整個作業全部由機器人處理, 可以精準的一箱箱搬到卡車上,卡車在根據排得精準的行程開往港口。 甚至我也在演算法交易的書上看過, 說最近幾年由於對於市場微結構的理解,還有電腦的進步,演算法的進步, 現在已經不像以前需要僱用那麼多交易員來處理每天的交易了。 像是常見的工作要把大單拆小慢慢丟到市場裡, 或是隨時監控不同交易所的執行條件作Routing執行等工作電腦作的已經非常好。 只要沒有碰到市場大風大浪,基本上是不太需要人參與的。 這樣就可以把交易手續費降到非常便宜,而開放API讓外面的人直接透過API交易也是這樣來的。 只要在碰到市場波動的時候再由明星交易員來手動開船就好。
再舉一個算是個人偏見的例子, 我認為現今的主流程式語言都太弱了,如果對於程式語言有一點點深入研究,會發現學界已經有很多厲害的東西但還沒普及。 如果能夠有一個足夠強的static type的語言讓大家使用,我認為可以減少非常多除錯的時間,讓整體生產力提昇。 現今的所標榜的各種Testing導向的開發,根本都是搶Compiler的工作來作,而且還作得沒有機器好,產生出一堆bug。 如果有一天我們能夠有一個很好的程式語言,夠強的Compiler,一間軟體公司根本可以減少許多測試,開發的人力。 甚至一個Compiler根本可以取代掉很多不合格的Programmers。 機器不需要作到完美,只需要作到足夠好就可以取代掉人類。
雖然我認為書中舉的一些資料是有爭議的, 至少不是能直接跳到作者宣稱的結論。 但我自己也相信在這個世代機器絕對會搶人的工作, 直到長期人類可以開創出另外的產業讓大家都能有工作。 有時候在想像是i-robot,real steel等電影中的未來世界,人們到底在作些什麼樣的工作呢? 假如有一天一個智慧型機器人便宜到唾手可得,就像現在的PC一樣,這樣的世界還有什麼樣的工作需要人作?
科技的成長速度在今後十年或許只會越來越快, 所謂的雲端運算我個人偏見認為或許稱為普及運算是更恰當, 今後十年運算資源會不斷地侵入生活中的每一個地方, 也許Google的無人駕駛車會讓很多物流系統自動化,海尼根的貨車現在還是人在開也變成無人駕駛。 Amazon的遞送系統不再有送貨員,無人駕駛車會自動開到你家, 並且在快到你家的時候自動用語音系統打一通電話請你出來收貨。 隨便你想到的一個東西都可能嵌有運算資源並配上用不盡的IPv6位址。 你吃完Pizza後可能連垃圾桶都智慧化,聯網來計算怎樣可以最有效的回收利用垃圾。
這樣的未來,也會加速所謂的資訊落差, 能夠掌握知識與資訊的人會佔盡優勢。 資本與人力的界線或許也會越來越模糊(智慧型機器人的用途究竟要算人力還是資本呢?) Iron Man 2裡面Whiplash在製造系統的時候曾說過一句話, 『人不可靠,人會犯錯,應該用遙控的』或許在未來這句話會越來越適用於這場人與機器的賽跑中。
I used to be an Haskeller like you, then I took an Arrow in the knee
You hardly can miss Arrow on your path of learning Haskell. Just after struggling with Functor, Applicative and Monad, you convince yourself that you can finally take a look at those standard libraries requiring you the knowledge of Monad. A few Arrow interface libraries such as Hakyll, HXT, reactive-banana just punch you in the face. You just don’t understand what that is. Finishing tutorials on wikibook (link1, link2) do help, but you still can’t get the whole picture. What’s the relationship between Arrow and Monad? Is there non-trivial concrete example that can persuade me it is useful? Here I try to provide my answers.
Why Monad is not Enough
Arrow is proposed by John Hughes in 1998. As described in his paper Generalising Monads to Arrows, the purpose of Arrows is to resolve the issue of memory consumption in using moandic parser. An example from the paper is:
instance MonadPlus Parser where
P a + P b = P (\s -> case a s of
Just (x, s') -> Just (x, s')
Nothing -> b s)The property of Plus corresponds to backtracking parsers. The input s is retained in the memory and not garbage collected as long as the parser a succeeding in parsing. If a succeeds a large part of the input s before it eventually fails, then a great deal of space would be used to hold these already-parsed tokens. To resolve this kind of problems, the Arrows was proposed.
Besides the issue mentioned above, We know that Monads essentially provide a sequential interface to computation. One can build a computation out of a value, or sequence two computations. The structure of Monads empowers us convenience and at the same time limits its usage. Some problem domains can not be modeled with Monads, jaspervdj proposes that a building system like Hakyll is one of them.
In general, the structure that is not sequental, but is much like electronic circuits can be modeled by Arrows. Monads fails to model these structures. Its composability is not as flexible as Arrows.
Typeclassopedia
Let’s see a diagram from Typeclassopedia by Brent Yorgey.

This diagram tells us the relationship between Monads and Arrows. Unlike Functor and Applicative, they are basically different things and from different lineage.
First of all, an Arrow has to be an Category. Category generalizes the notion of function composition to the morphisms in Category Theory. Its definition in base package is as follows:
class Category cat where
id :: cat a a
(.) :: cat b c -> cat a b -> cat a cWe can see that it requires an identity morphism id, and the composition operator (.) for morphisms. Also note that Category is unequivalent to arbitrary categories in Category Theory. It only corresponds to those categories whose objects are objects of Hask.
Laying on the foundation of Category, Arrow’s definition is as follows:
class Category a => Arrow a where
arr :: (b -> c) -> a b c
first :: a b c -> a (b, d) (c, d)
second :: a b c -> a (d, b) (d, c)
(***) :: a b c -> a b' c' -> a (b, b') (c, c')
(&&&) :: a b c -> a b c' -> a b (c, c')There are five methods here, but actually you only have to define arr and first. Rest of them can be automatically derived.
To see how these five composing methods work, let’s try out an easy example. That is to model an OR gate with NAND gates.
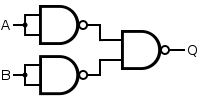
We can duplicate the input to the first level NAND gates with id and &&&, and to combine the results of first level NAND gates, we can use *** operator. In chart it looks like this.
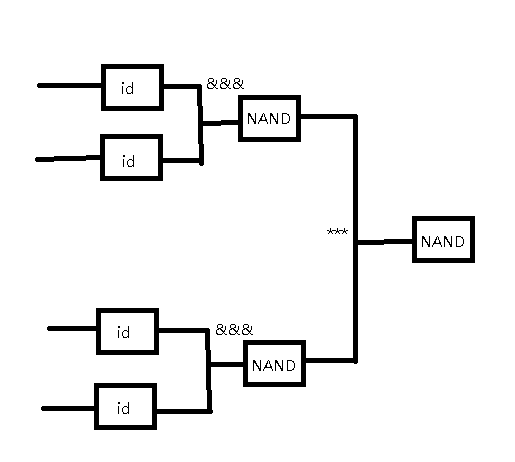
To implements it in haskell we also need to define the circuit element as instances of Category and Arrow, we call it Auto.
{-# LANGUAGE Arrows #-}
import Prelude hiding (id, (.))
import Control.Arrow
import Control.Category
data Auto b c = Auto (b -> c)
instance Category Auto where
id = Auto id
Auto f . Auto g = Auto (f . g)
instance Arrow Auto where
arr f = Auto f
first (Auto f) = Auto $ \(x, y) -> (f x, y)
nand2 :: Auto (Bool, Bool) Bool
nand2 = arr (not . uncurry (&&))
or2 :: Auto (Bool, Bool) Bool
or2 = ((arr (id) &&& arr (id)) >>> nand2) *** ((arr (id) &&& arr (id)) >>> nand2) >>> nand2
runAutoA :: (Bool, Bool) -> Auto (Bool, Bool) a -> IO a
runAutoA x (Auto f) = return (f x)
main = do
let comb = [(False, False), (False, True), (True, False), (True, True)]
result <- sequence $ flip runAutoA or2 `map` comb
putStrLn $ show resultArrow Notation
When we are tackling larger problems, the notation soon gets complicated to handle. That’s why we want to have do block syntax sugar to make it look nicer, as we do for Monad. GHC provides Arrow Notation, but it’s currently not part of Haskell 98, you must enable the corresponding extension: with -XArrow or prepend a header line to the files {-# LANGUAGE Arrows #-}. After that, we can rewrite our OR gate example above with Arrow notation.
{-# LANGUAGE Arrows #-}
import Prelude hiding (id, (.))
import Control.Arrow
import Control.Category
data Auto b c = Auto (b -> c)
instance Category Auto where
id = Auto id
Auto f . Auto g = Auto (f . g)
instance Arrow Auto where
arr f = Auto f
first (Auto f) = Auto $ \(x, y) -> (f x, y)
nand2 :: Auto (Bool, Bool) Bool
nand2 = arr (not . uncurry (&&))
or2' :: Auto (Bool, Bool) Bool
or2' = proc (i0, i1) -> do
m1 <- nand2 -< (i0,i0)
m2 <- nand2 -< (i1,i1)
nand2 -< (m1,m2)
runAutoA :: (Bool, Bool) -> Auto (Bool, Bool) a -> IO a
runAutoA x (Auto f) = return (f x)
main = do
let comb = [(False, False), (False, True), (True, False), (True, True)]
result' <- sequence $ flip runAutoA or2' `map` comb
putStrLn $ show result'The pattern is keyword proc followed with the input symbols, then -> do. We describe each elemment in each line. m1 <- nand2 -< (i0,i0) means nand2 accept a tuple (i0, i0) and the its output is bound to the name m1. The last line must be an expression, just like Monad, its value denotes the value of the whole do block. In this case, its the output of nand2 -< (m1,m2)
A More Complicated Example
Already know how to simulate OR with NAND, let’s implement a hald-adder.
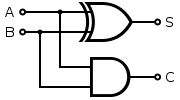
With the help of Arrow Notation, all we need to do is to define the instances, and drawing circuits with <- and -< symbols in the program.
{-# LANGUAGE Arrows #-}
import Prelude hiding (id, (.))
import Control.Arrow
import Control.Category
data Auto b c = Auto (b -> c)
instance Category Auto where
id = Auto id
Auto f . Auto g = Auto (f . g)
instance Arrow Auto where
arr f = Auto f
first (Auto f) = Auto $ \(x, y) -> (f x, y)
and2 :: Auto (Bool, Bool) Bool
and2 = arr (uncurry (&&))
or2 :: Auto (Bool, Bool) Bool
or2 = arr (uncurry (||))
nand2 :: Auto (Bool, Bool) Bool
nand2 = arr (not . uncurry (&&))
xor2 :: Auto (Bool, Bool) Bool
xor2 = proc i -> do
m0 <- nand2 -< i
m1 <- or2 -< i
and2 -< (m0, m1)
hAdder :: Auto (Bool, Bool) (Bool, Bool)
hAdder = proc i -> do
o0 <- xor2 -< i
o1 <- and2 -< i
id -< (o1, o0)
runAutoA :: (Bool, Bool) -> Auto (Bool, Bool) a -> IO a
runAutoA x (Auto f) = return (f x)
main = do
putStr "Hello "
pairs <- runAutoA (True, True) hAdder
putStrLn $ show pairsPostscript
As you can see from typeclassopedia diagram, there are variants of Arrow. They are ArrowZero, ArrowPlus, ArrowLoop, ArrowChoice and ArrowApply, where ArrowApply is equivalent to Monad. I’ll write another post to introduce them another days.